PANCE Blueprint GI and Nutrition (8%)

61 y/o with acute onset severe abdominal pain and vomiting

Patient with small bowel obstruction will present as → a 55-year-old male presents to the emergency department with a two-day history of severe abdominal pain, vomiting, and inability to pass stool or gas. He describes the pain as crampy and worsening, localized initially around the umbilicus but now diffused across the abdomen. His medical history is significant for an open appendectomy 20 years ago. On examination, his abdomen is distended and tender with high-pitched, tinkling bowel sounds. He is afebrile, but his heart rate is elevated. An abdominal X-ray reveals dilated loops of small bowel with air-fluid levels. You note valvulae conniventes across the full width of the bowel suggestive of a small bowel obstruction. A CT scan of the abdomen confirms the diagnosis, showing a transition point with no evidence of strangulation. The patient is admitted for nasogastric decompression, intravenous fluids, and bowel rest. Surgery is consulted for potential operative intervention, given his history of previous abdominal surgery and the likelihood of adhesive disease. The patient is closely monitored for signs of bowel ischemia or perforation.

Small Bowel Obstruction (SBO)

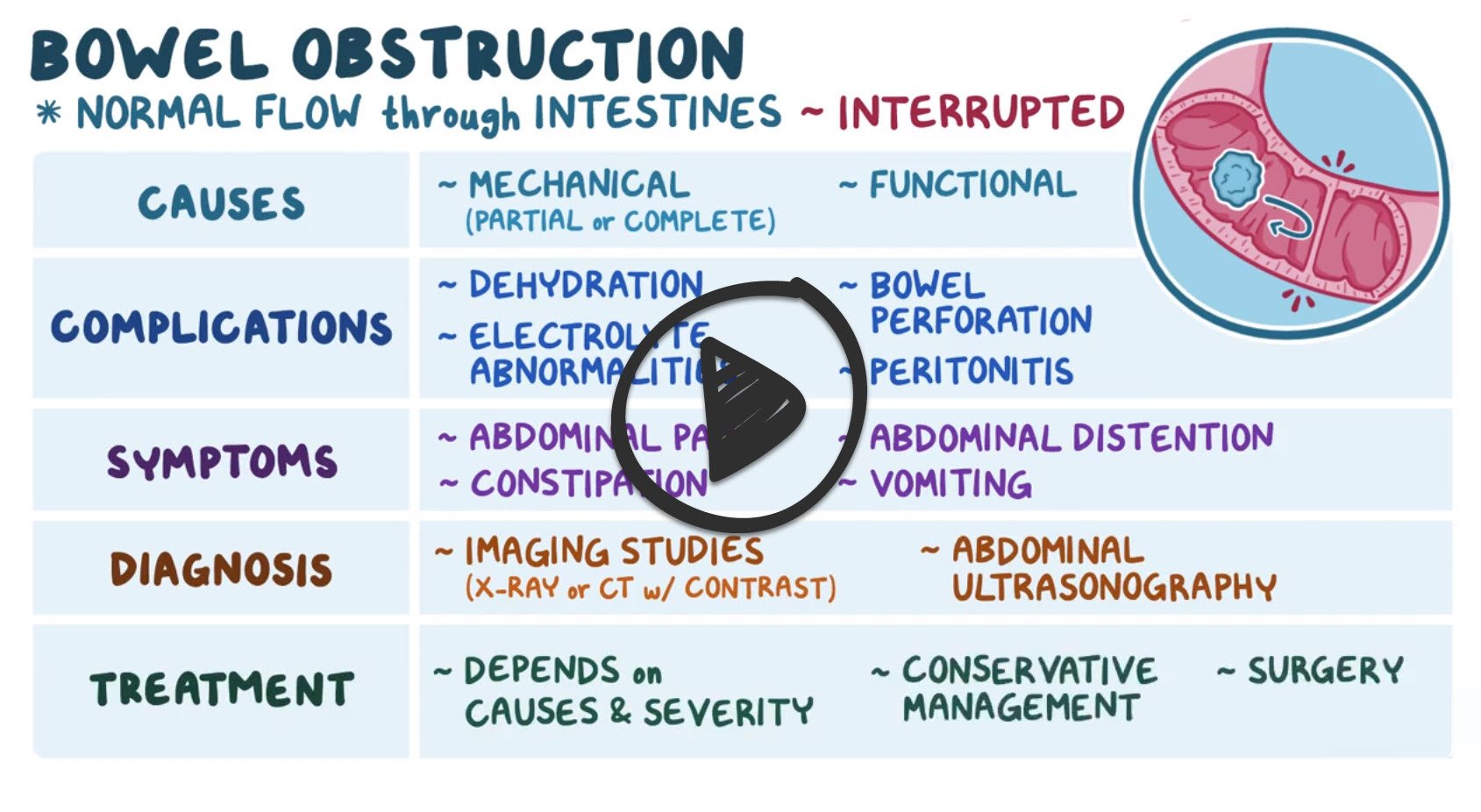
• Small bowel obstruction presents with abdominal pain, distention, vomiting of partially digested food, and obstipation
• Bowel sounds are high-pitched and come in rushes. Later in the process, the bowel becomes silent
• Most small bowel obstructions are due to mechanical obstructions caused by adhesions or hernias; other causes include neoplasm, intussusception, foreign body, inflammatory bowel disease, and volvulus
• Functional causes of SBO include postoperative ileus (transient paralysis of smooth muscle), infection or inflammation, hypothyroidism, electrolyte abnormalities (hypokalemia and hypercalcemia), and medications (i.e. opioids)
• Intussusception is the most common cause in children
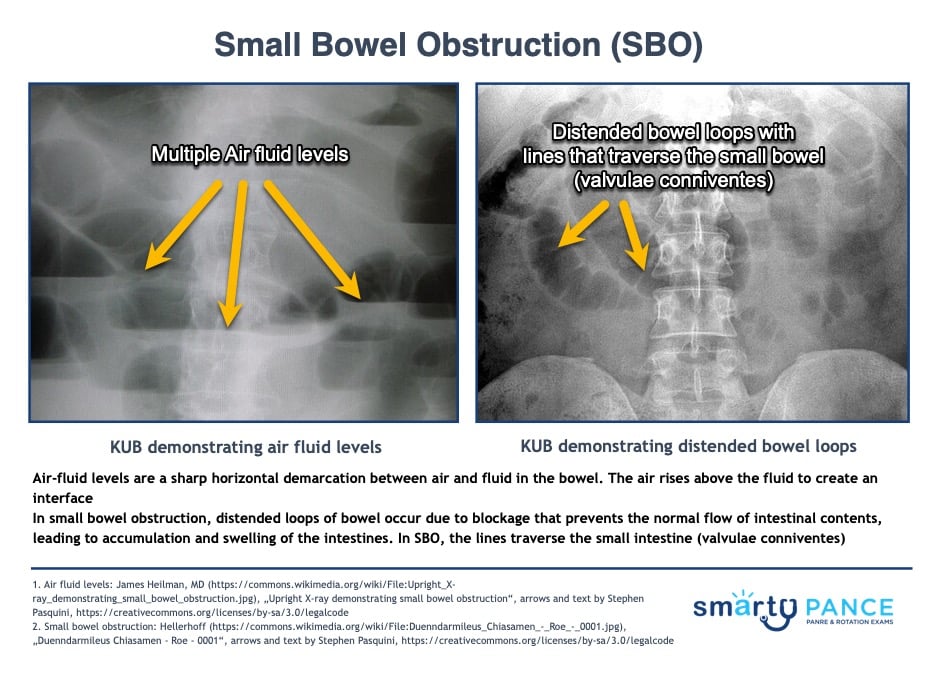
• KUB shows dilated loops of bowel with air-fluid levels with little or no gas in the colon.
• Treat with decompression with an NGT, surgery if a mechanical obstruction is suspected

"Early versus late obstruction: Obstipation and absent bowel sounds are seen late in intestinal obstruction. Hyperactive bowel sounds are very common early in the course of intestinal obstruction. They are described as high-pitched with occasional rushes."

Large Bowel Obstruction (LBO)

• MCC: cancer, strictures, hernias, volvulus, and fecal impaction
• Obstruction is typically in the colon or rectum
• Symptoms include gradually increasing abdominal pain with longer intervals between episodes of pain, abdominal distention, constipation, less nausea and vomiting (may be delayed) - late-onset feculent vomiting, blood in stool, more common in the elderly
• Patients may be febrile and tachycardia => shock may ensue
• Dehydration + electrolyte imbalances

DX: Obtain plain radiographs to quickly confirm a diagnosis of bowel obstruction, and, provided the films do not have findings that indicate the need for immediate intervention, then use computed tomography (CT) of the abdomen and pelvis to further characterize the nature, severity, and potential etiologies of the obstruction

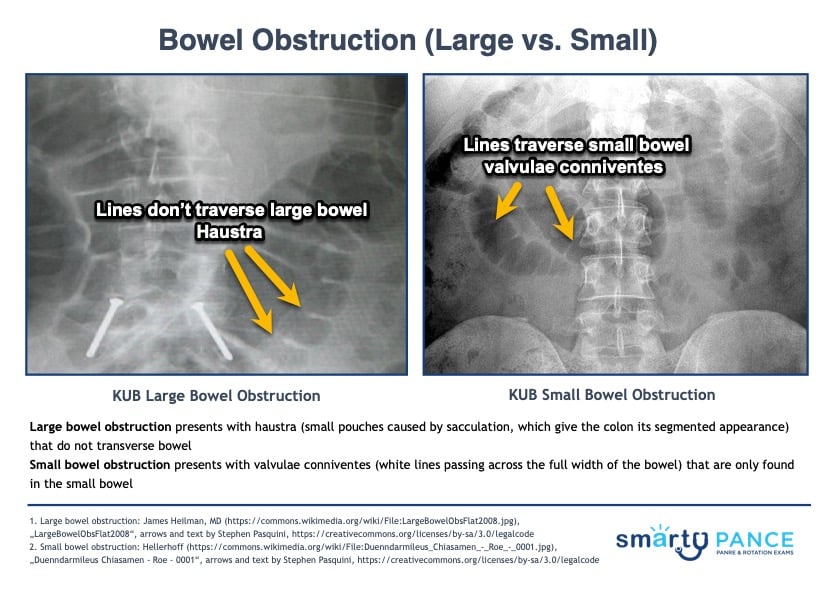
• KUB shows dilated colon (> 5 cm), air-fluid levels in the colon, haustra (small pouches caused by sacculation, which give the colon its segmented appearance) that do not transverse bowel, bird beak sign: narrowing of the lumen at the site of obstruction

TX: Bowel rest, NG tube placement, surgery as directed by the underlying cause

Upright radiographs may demonstrate the following:

• Small Bowel Obstruction: KUB shows dilated loops of bowel with air-fluid levels with little or no gas in the colon
• Large bowel obstruction: KUB shows dilated large intestine

Additional imaging includes an abdominal CT scan with contrast in order to identify the potential cause of obstruction. Abdominal ultrasonography may be useful for individuals with contraindications to CT scanning, like those with contrast allergies and pregnant females.

Treatment includes hospitalization, IV fluids, nothing by mouth, and nasogastric suctioning to remove the fluid and gasses that have built up

• Urgent surgical consultation is necessary when a mechanical obstruction is suspected